Properties Example

\rho = \{ \frac{p}{q}, \frac{q}{p} \}

• Is symmetric, is not reflexive or transitive

Functions (Mappings)

Let S and T be sets. S = \{ (1,2) \} \qquad T = \{ a,b,c \}

A function f from S to T (f:S \to T) is a subset of S \times T (f \subseteq S \times T)

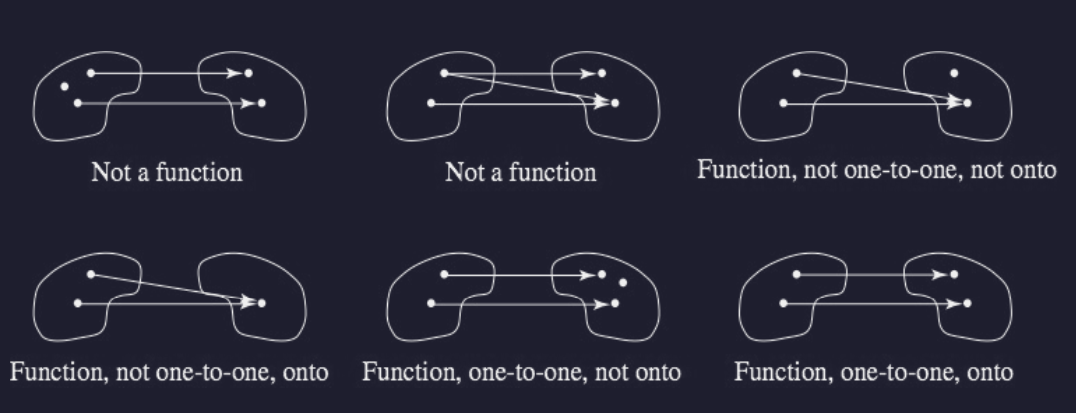
• Each member of S can appear only once as the first component of an ordered pair.
  • Suppose (s,t) belongs to the function, then t can be denoted by f(s)
    • Preimage: s (“preimage of t under f”)
    • Image: t (“image of s under f”)
• Domain: S
• Codomain: T
• Range: f(s) \subseteq T
  • Set of images smaller than the codomain

For A \subseteq S, f(A) denotes \{ f(a) | a \in A \}

Summary: Three Parts of a Function

1. A set of starting values
2. A set from which associated values come
3. The association itself

These rules for a function mean that functions can’t have a binary relation that is one-to-many or many-to-many.

Floor Function and Ceiling Function

Floor Function: floor(x)$

• Associates with each real number x the greatest integer less than or equal to x

Ceiling Function: ceil(x)

• Associates with each real number x the smallest integer greater than or equal to x.

Note: Both floor and ceil domains’ are all real numbers.

Equal Functions

Equal Functions: Two functions are equal if they have the same:

1. Domain,
2. Codomain, and
3. Association of values

Example: Suppose:

• g: R \to R, where g(x) = x^3
• f: Z \to R, given by f(x) = x^3

Then:

• f is not the same function as g, because g has a different domain than f (all real numbers \ne all real integers)
  • e.g., g can have (1.1, 1.331) while f cannot

Onto (Surjective) Functions

Onto Function: Function where the range of f equals the codomain of f

• “Every node has an association”

To prove that a given function is onto:

1. Show that T \text{(domain)} \subseteq R \text{(range)} (this proves that R = T)
2. Show that an arbitrary member of the codomain is a member of the range.

One-to-One (Injective) Functions

One-to-one Function: Function (f:S \to T) where no member of T is the image under f of two distinct elements of S.

To prove that a function is one-to-one, we assume that there are elements s_1 and s_2 of S with f(s_1) = f(s_2) and then show that s_1 = s_2

Bijective Functions

Bijective Function: Function (f: S \to T) that’s both one-to-one and onto.

Composition of Functions

Suppose f: S \to T and g: T \to U

Composition Function: Function (g \circ f) from S to U defined by (g \circ f)(s) = g(f(s))

• Applied right-to-left (f applied, then g)
• Preserves properties of being onto and one-to-one.

Theorem on Composing Two Bijections: The composition of two bijections is a bijection.

• Ergo, suppose f: S \to T and g: T \to U are onto, then g \circ f is also onto.

Next Lecture

Next lecture (Tuesdau) will be a review section.

Each student can choose one of the four homework and make it up.

• A new list of questions will be given and answers will be turned in via paper on next Thursday.

Finals will probably be graded within a day because Prof. has to travel lol.

Composition of Functions Cont.

Suppose f: S \to T and g: T \to U

Composition Function: Function (g \circ f) from S to U defined by (g \circ f)(s) = g(f(s))

• Applied right-to-left (f applied, then g)
• Preserves properties of being onto and one-to-one.

Theorem on Composing Two Bijections: The composition of two bijections is a bijection.

• Ergo, suppose f: S \to T and g: T \to U are onto, then g \circ f is also onto.

Example: R \to R, f(x)=x^2 \qquad R \to R, g(x) = x-1 f \circ g(x) = (x-1)^2 \qquad g \circ f(x) = x^2 - 1

Inverse Functions

Identity Function: Function that maps each element of a set S to itself, leaving each element of S unchanged (i_s).

• Suppose f: S \to S is a bijection.
  • Because f is onto, every t \in T has a preimage in S.
    • Because f is one-to-one, each preimage is unique

Inverse Function:

• Suppose f: S \to T and g: T \to S such that g \circ f = i_s and f \circ g = i_p; then g is the inverse function of f, denoted for f^{-1}

Theorem on Bijections and Inverse Functions:

• If f:S \to T, then f is a bijection if and only if f^{-1} exists

Example: Suppose S = \{ 1,2,3 \} and T = \{ a,b,c \}, and that

• S \to T: f = \{ (1,a), (2,b), (3,c) \}
• T \to S: g = \{ (a,1), (b,2), (c,3) \}

Then:

• f \circ g = \{ (a,a), (b,b), (c,) \} = i_T
• g \circ f = \{ (1,1), (2,2) (3,3) \} = i_S

Example: Suppose S = \{ 1,2,3 \} and T = \{ a,b,c \}, and that

• S \to T: f = \{ (1,a), (2,b), (3,b) \}

Identifying f:

• This is not one-to-one because b gets connected-to twice.
• This is not onto because C isn’t used.
  • Remember the layman definition of onto function: “Every node has an association”

Example: Suppose S = \{ 1,2,3 \} and T = \{ a,b,c \}, and that

• S \to T: f = \{ (1,a), (2,b), (3,c) \}

Identifying f:

• This is one-to-one because each thing has at most one mapping
• This is onto because every ode is mapped
• Thus, this is a bijection.